1322. Произведение матриц

В лесу графини Мордвиновой. Петергоф. 1891. С годами у художника развилось обостренное цветовое видение. Теперь он видит и может передать кистью изменчивость цветов в зависимости от освещения и от рефлексов соседних предметов. Живописец выписывает мягкие переходы зеленых, желтоватых и сероватых оттенков стволов елей, хвои и мха. Но тонкие колористические изменения не самоцель для художника: ими он стремится донести до зрителя реальную жизнь природы. Картина вызывает у зрителя впечатление, что он находится внутри лесного пространства, дает прочувствовать окружающую атмосферу сосновой чащобы.

Даны три квадратные матрицы A, B, C, каждая из которых имеет размер n ´ n. Необходимо проверить равенство: A ´ B = C.

Вход. Каждый тест начинается значением n (n £ 500). Далее следуют три матрицы A, B, C, каждая из которых представляется n строками, содержащих в точности n чисел. Элементы матриц А и В по модулю не превышают 1000. Последний тест содержит n = 0 и не обрабатывается. Например, в первом тесте следует проверить равенство

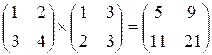
Выход. Для каждого теста в отдельной строке вывести “YES” или “NO” в зависимости от того, имеет ли место равенство A ´ B = C или нет.

Пример входа	Пример выхода
2 1 2 3 4 1 3 2 3 5 9 11 21 2 1 2 3 4 1 3 2 3 5 9 10 21 0	YES NO

РЕШЕНИЕ

теория вероятности

Анализ алгоритма

Тесты были подобраны так, что простое умножение матриц с временной оценкой O(n³) дает Time Limit. Задачу следует решать вероятностным методом.

Сгенерируем вектор r длины n из 0 и 1. Вычислим вектора ABr = A(Br) и Cr за O(n²). Если они равны, то с вероятностью 50% можно сказать, что A ´ B = C. Проведем такое тестирование, например, 10 раз. Тогда с вероятностью 1 – 1/2¹⁰ получим правильный ответ.

ABr вычисляется так (умножение матриц и векторов ассоциативно): сначала умножаем матрицу B на вектор r за O(n²), получаем вектор. Потом множим матрицу А на этот вектор опять за время O(n²).

Реализация алгоритма

Объявим рабочие массивы.

#define MAX 501

int a[MAX][MAX], b[MAX][MAX], c[MAX][MAX], r[MAX], r1[MAX], r2[MAX];

Читаем входные данные для каждого теста. Последний тест содержит n = 0 и не обрабатывается.

while (scanf("%d", &n), n)

{

for (i = 0; i < n; i++)

for (j = 0; j < n; j++) scanf("%d", &a[i][j]);

for (i = 0; i < n; i++)

for (j = 0; j < n; j++) scanf("%d", &b[i][j]);

for (i = 0; i < n; i++) for (j = 0; j < n; j++)

scanf("%d", &c[i][j]);

Для каждого теста проверку равенства ABr = Cr производим 10 раз.

for (cnt = 0; cnt < 10; cnt++)

{

Заполняем линейный массив r нулями и единицами произвольным образом.

for (flag = i = 0; i < n; i++) r[i] = rand() % 2;

Выполняем умножение r₁ = Br.

for (i = 0; i < n; i++)

for (r1[i] = k = 0; k < n; k++) r1[i] += b[i][k] * r[k];

Выполняем умножение r₂ = Ar₁ = ABr.

for (i = 0; i < n; i++)

for (r2[i] = k = 0; k < n; k++) r2[i] += a[i][k] * r1[k];

Выполняем умножение r₁ = Cr.

for (i = 0; i < n; i++)

for (r1[i] = k = 0; k < n; k++) r1[i] += c[i][k] * r[k];

Сравниваем массивы r₂ и r₁. То есть проверяем равенство ABr = Cr. Если ABr ≠ Cr, то устанавливаем flag = 1.

for (i = 0; i < n; i++)

if (r1[i] != r2[i])

{

flag = 1; break;

}

if (flag) break;

}

Для текущего теста выводим ответ.

if (flag) printf("NO\n"); else printf("YES\n");

}